Área de figura plana es una medida de extensión de una superficie. En las áreas de superficie planas o polìgonos que son superficies planas de lados rectos; estas pueden triangularse para obtener sus áreas. Entre los polígonos tenemos: el triángulo, rectángulo, rombo,cuadrado, romboide, trapecio,etc.
Área del rectángulo: es el área más sencilla para calcular. Es el resultado de multiplicar la longitud de sus lados o también, como se dice habitualmente, se obtiene multiplicando la base (b) por la altura (h).
Fórmula: Área del rectángulo = base · altura A = b · h

Área del paralelogramo: Si consideramos el paralelogramo ABCD. La base AB desde C y D se hacen perpendiculares sobre la base AB.
Los triángulos ADM y BCN son iguales. Por tanto, el área del paralelogramo ABCD es la misma que la del rectángulo MNCD. Observamos que las dos figuras tienen la misma base y la misma altura. Este proceso nos permite afirmar que el área de un paralelogramo es, también, el producto de su base por su altura.
Fórmula: Área del paralelogramo = base · altura A = b · h
Área del cuadrado: en un cuadrado la base y la altura son iguales a su lado y por tanto:
Fórmula: Área del cuadrado de lado c = lado al cuadrado A = c2

Área del triángulo: consideremos un triángulo cualquiera ABC, de base AB. Dibujemos una paralela a AB que pase por C y una paralela a AC que pase por B. Éstas se encuentran en un punto D.
El área de las figuras planas
Los triángulos ABC y BCD serán iguales. Por tanto, la superficie del paralelogramo ABCD será el doble del área del triángulo ABC.
Fórmula: Área del paralelogramo ABCD = 2 · área del triángulo ABC
O bien,
Área del triángulo ABC = área del paralelogramo : 2
Como la base y la altura del paralelogramo son la base y la altura del triángulo obtendremos:
Fórmula: Área del triángulo = base por altura dividido por 2 / A = b · h : 2

Pasos para calcular el áre a de un hexágono
Antes que nada tenemos que tener claro que para hacer el cálculo es mejor que sepamos los valores tanto del perímetro como de otra función o potencia que también vamos a explicaros de modo que atentos a todos los datos que aportemos.
Una forma de encontrar el área de un hexágono regular (es decir, de lados iguales) es dividiéndolo primero en triángulos equiláteros. También necesita usar una apotema, un segmento que une el centro de un polígono regular con el punto medio de cualquier lado y que es perpendicular a ese lado.
Calcular la apotema
Para calcular el área necesitas saber primero el valor de la apotema de modo que debes hacer lo siguiente:
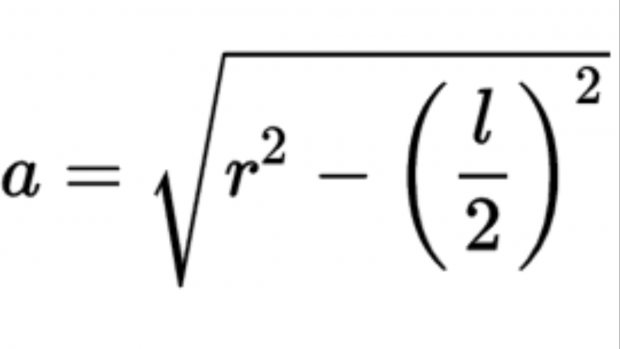
Fórmula para calcular la apotema En esta fórmula, los valores de cada letra son:
- a: el valor de la apotema del hexágono
- l: la medida de uno de los lados del polígono regular
- r: al ser un hexágono, tenemos que anotar también la longitud del lado del hexágono.
La igualdad de l=r hace que que la fórmula anterior la podamos hacer más fácil de forma que podemos calcular la apotema de un hexágono regular a partir de la resolución de esta otra ecuación que vemos a continuación:
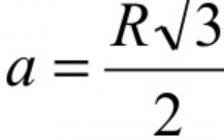
Fórmula para calcular la apotema Calcular el área
Para calcular el área del hexágono una vez conocemos la apotema ya solo nos queda aplicar esta fórmula:
- Área del hexágono = 3 · lado · apotema
Por lo tanto, lo único que tendrás que hacer es averiguar cuál es el valor del triple de la multiplicación de uno de los lados por la apotema del hexágono regular.
¿Y si no tenemos la apotema?
Si no sabemos cuál es el valor de la apotema del hexágono, siempre se puede calcular el área con esta otra fórmula:
- Área = 2,60 · L2
Últimas conclusiones
Tenemos que añadir que para problemas con hexágonos, el uso de los triángulos equiláteros y triángulos de 30 ° – 60 ° – 90 ° a menudo son útiles. Un hexágono regular se puede cortar en seis triángulos equiláteros, y un triángulo equilátero se puede dividir en dos triángulos de 30 ° – 60 ° – 90 °. Entonces, si estas haciendo un problema de hexágono, puedes cortar la figura y usar triángulos equiláteros o triángulos de 30 ° – 60 ° – 90 ° para ayudarte a encontrar la apotema, el perímetro o el área.
El área del círculo es igual al valor de su radio elevado al cuadrado multiplicado por pi = p x r2.
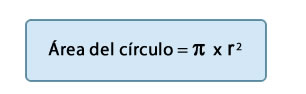
Ejemplo:
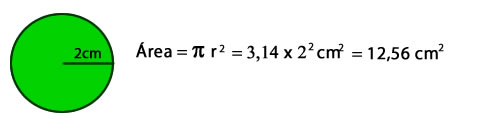
Comentarios
Publicar un comentario